Dieses Verfahren wurde 1925 von Warren L. McCabe und Ernest Thiele veröffentlicht.
Es ist eine sehr einfach zu verstehende graphische Methode zur Planung von Destillationen. Dabei geht es primär um die für die Industrie wichtigen kontinuierlichen Destillationssysteme. Aber auch auf nicht-kontinuierliche Systeme wie unsere Refluxdestillen ist die Methode übertragbar und dabei sogar noch einfacher verständlich.
Das Wertvolle dabei ist, daß man damit die Refluxmenge in Rechnungen einbezieht. Also zum Beispiel daß man berechnen kann, wie die Alkoholstärke des Destillats sinkt, wenn man der Kolonne oben mehr Produkt entnimmt, also den Reflux zurück in die Kolonne reduziert.

Die Konstruktion eines McCabe-Thiele-Diagramms für eine nicht-kontinuierliche Destille:
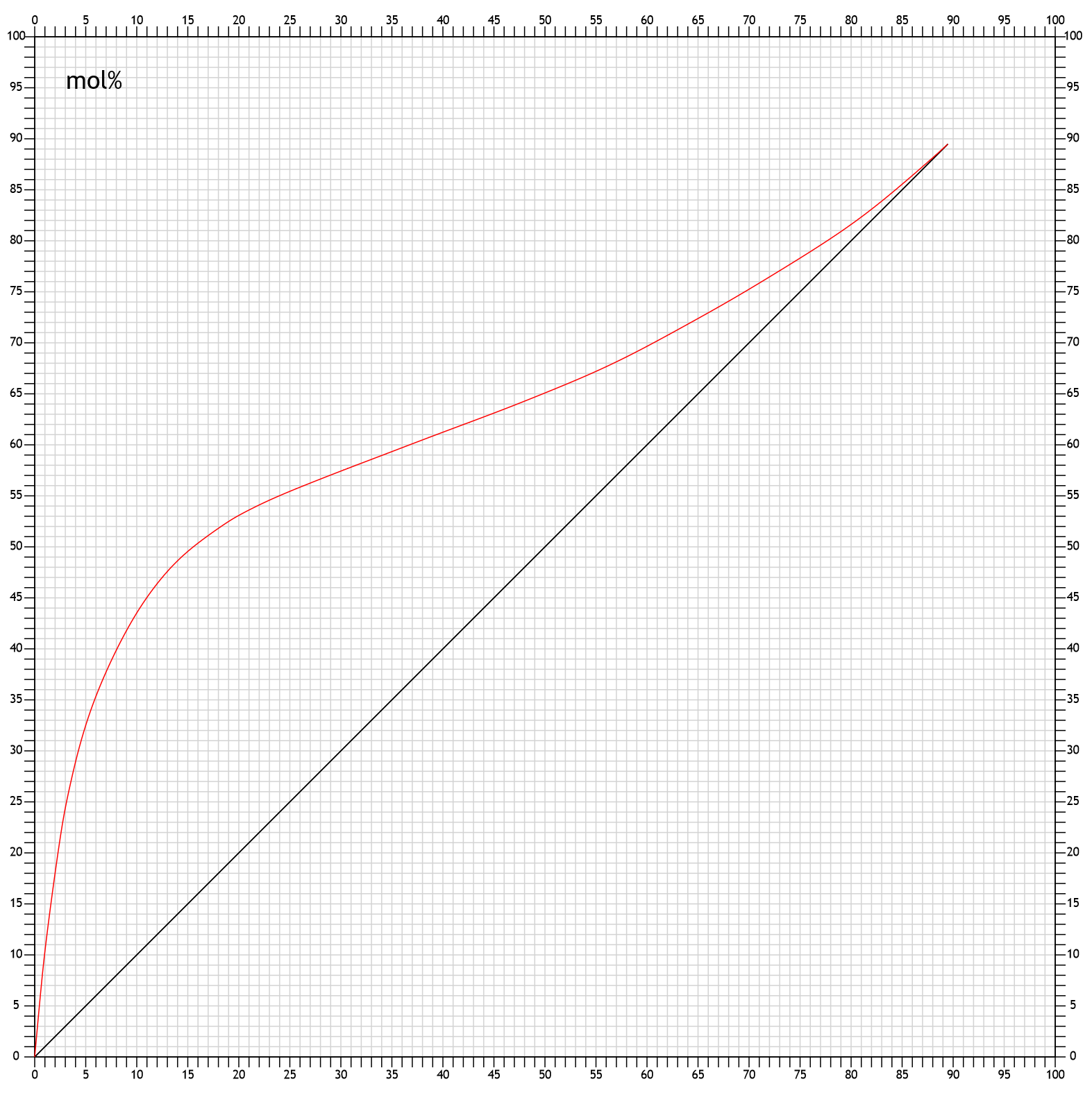
Ein McCabe-Thiele-Diagramm beginnt mit der Kurve x = Alkohlstärke in der Destille und y = Alkoholstärke im Destillat, also einer Siedediagrammkurve, und einer schrägen Linie bei x = y: Dann wird die Zielalkoholstärke im Destillat als senkrechte Linie von unten nach oben bis zur schrägen Gerade eingetragen. Im nächsten Bild bei x = 70mol%. Und dann wird ausgehend vom erreichten Punkt nach links eine sogenannte "Arbeitsgerade" eingezeichnet. Ihr Winkel bezeichnet das Rückflussverhältnis. Geht sie waagerecht nach links, bedeutet das 0% Reflux, also eine Potstill oder eine Refluxdestille mit abgeschaltetem Reflux. Geht sie nach links 45° nach unten, liegt sie also auf der schwarzen schrägen Gerade, bedeutet das 100% Reflux. Winkel außerhalb dieses Bereichs sind nicht möglich. Genau in der Mitte zwischen waagerecht und 45°, also bei 22.5°, bedeutet das 50% Reflux. So ist es hier auch eingezeichnet: Und nun werden die realen Böden als Stufen eingezeichnet und am Schluss eine Linie ganz nach unten gezogen. Angenommen, die Destille hat 5 reale Böden oder das Äquivalent in Packungshöhe, sieht das so aus: Die linke grüne Linie ist bei etwa x = 12mol%.
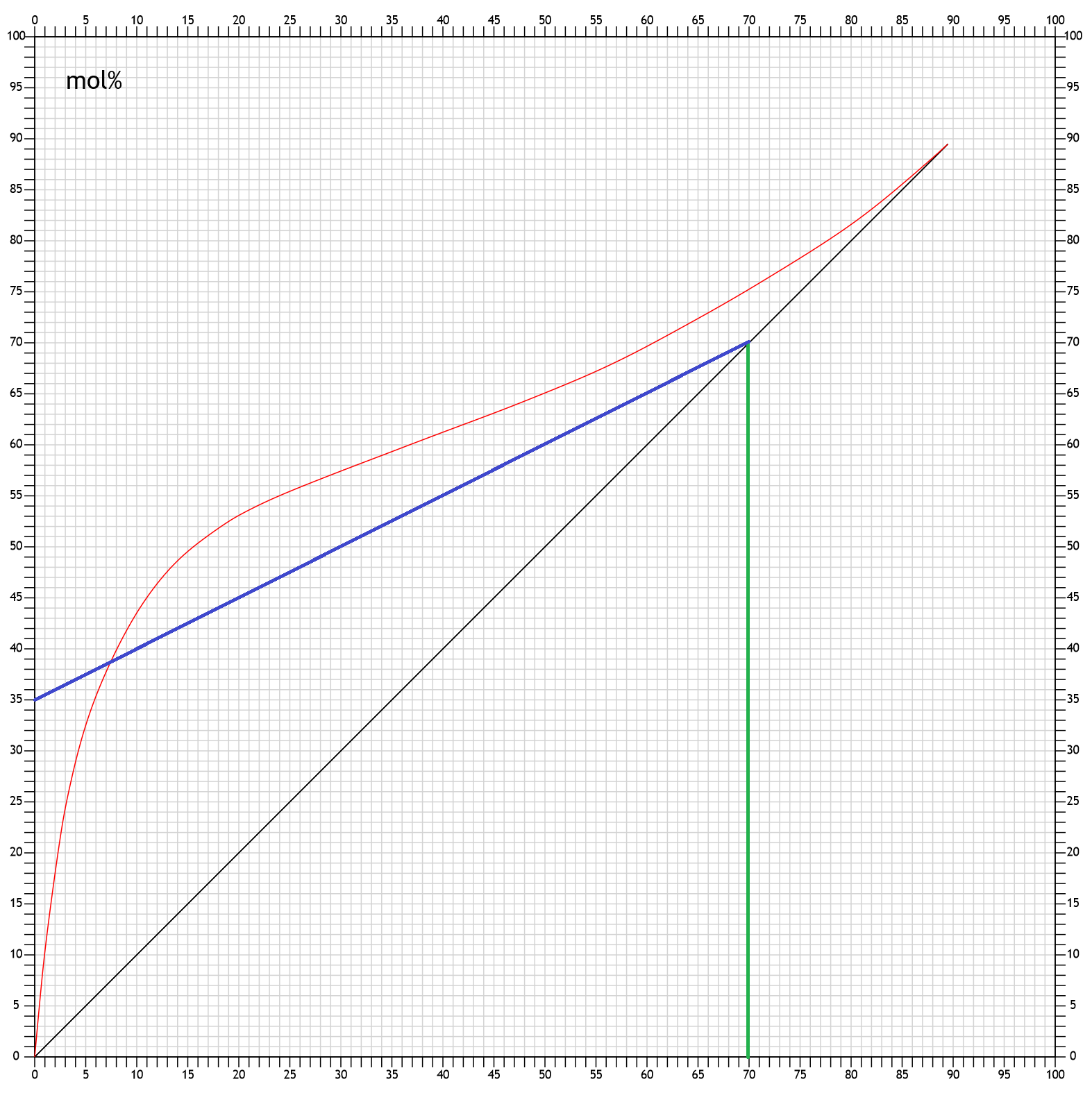
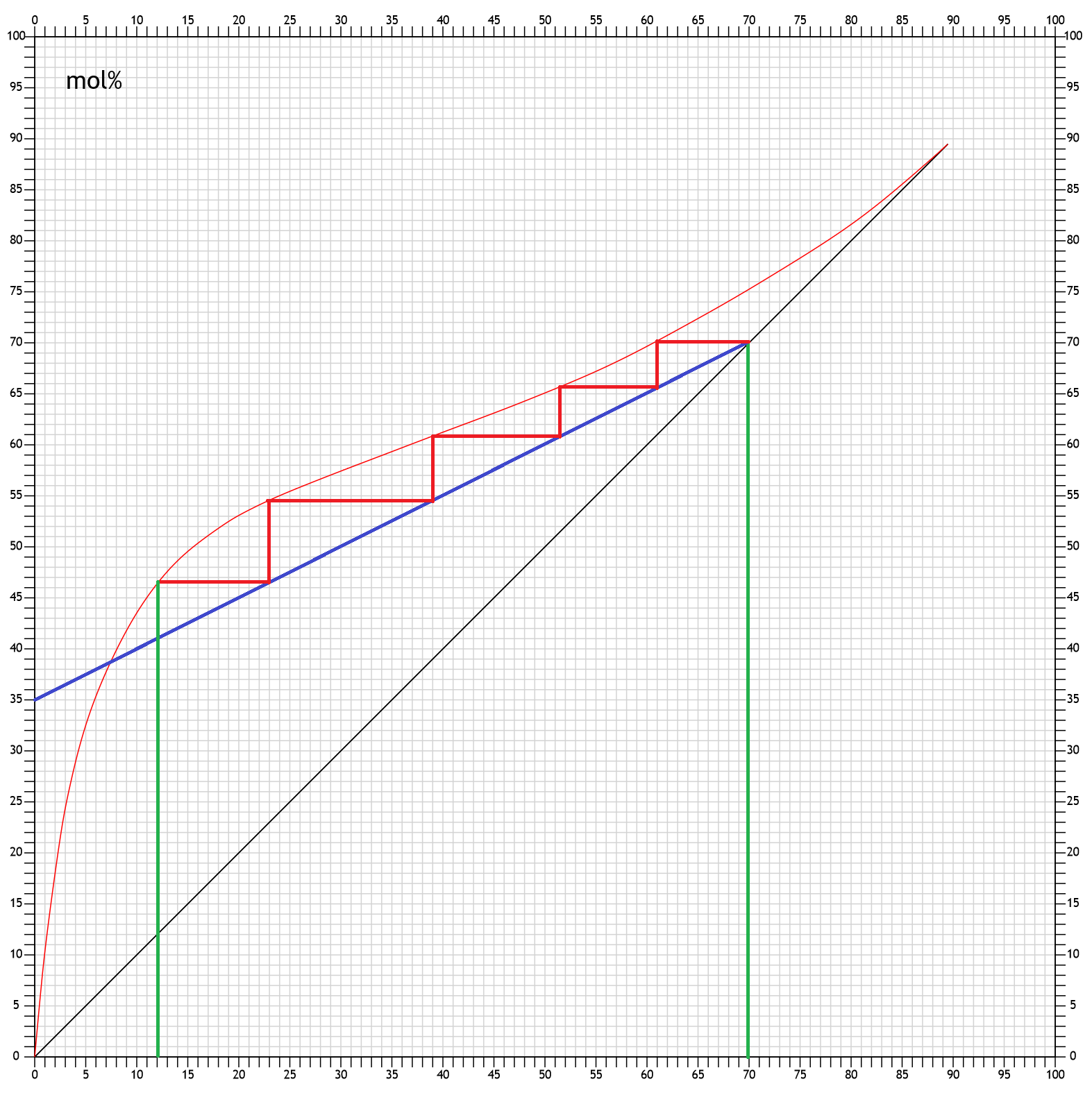
Das Ergebnis ist also:
Um bei 50% Reflux (also einem Reflux Ratio von 1) mit 5 Böden auf 70mol% zu kommen, braucht man 12mol% in der Destille.
Oder:
Hat man 12mol% in einer Destille mit 5 Böden, dann bekommt man mit 50% Reflux ein Destillat mit 70mol%.
So herum kann man das Diagramm aber nicht konstruieren. Man muss es immer ausgehend von einer Destillatsalkoholstärke konstruieren. Um von einer Kessel-Alkoholstärke die Destillats-Alkoholstärke berechnen zu können, muss man iterieren. Also man muss das Ergebnis schätzen, dann wie vorgegeben von der Destillats-Alkoholstärke die Stufen nach unten rechnen, mit dem Ergebnis die anfängliche Schätzung korrigieren, wieder nach unten überprüfen, usw. Das gleiche gilt, wenn man aus den beiden Alkoholstärken und den realen Böden die nötigen % Reflux berechnen will oder aus den beiden Alkoholstärken und den % Reflux die benötigten realen Böden.

Die minimalen % Reflux
Ein interessanter Punkt in dem Diagramm ist die Stelle, wo die blaue Arbeitsgerade die Siedediagrammkurve schneidet. In unserem Diagramm ist das etwa bei 7.5mol% in der Destille. Über diesen Punkt können die Stufen nicht hinaus. Also selbst unendlich Stufen würden nicht tiefer als x = 7.5mol% gehen: Das bedeutet: Egal wie viele Böden man hat, man braucht mindestens 7.5mol% im Kessel, um mit 50% Reflux 70mol% im Destillat zu bekommen. Oder: Um mit niedrigerer Alkoholstärke im Kessel 70mol% im Destillat zu bekommen, muss zwingend der Reflux erhöht werden.
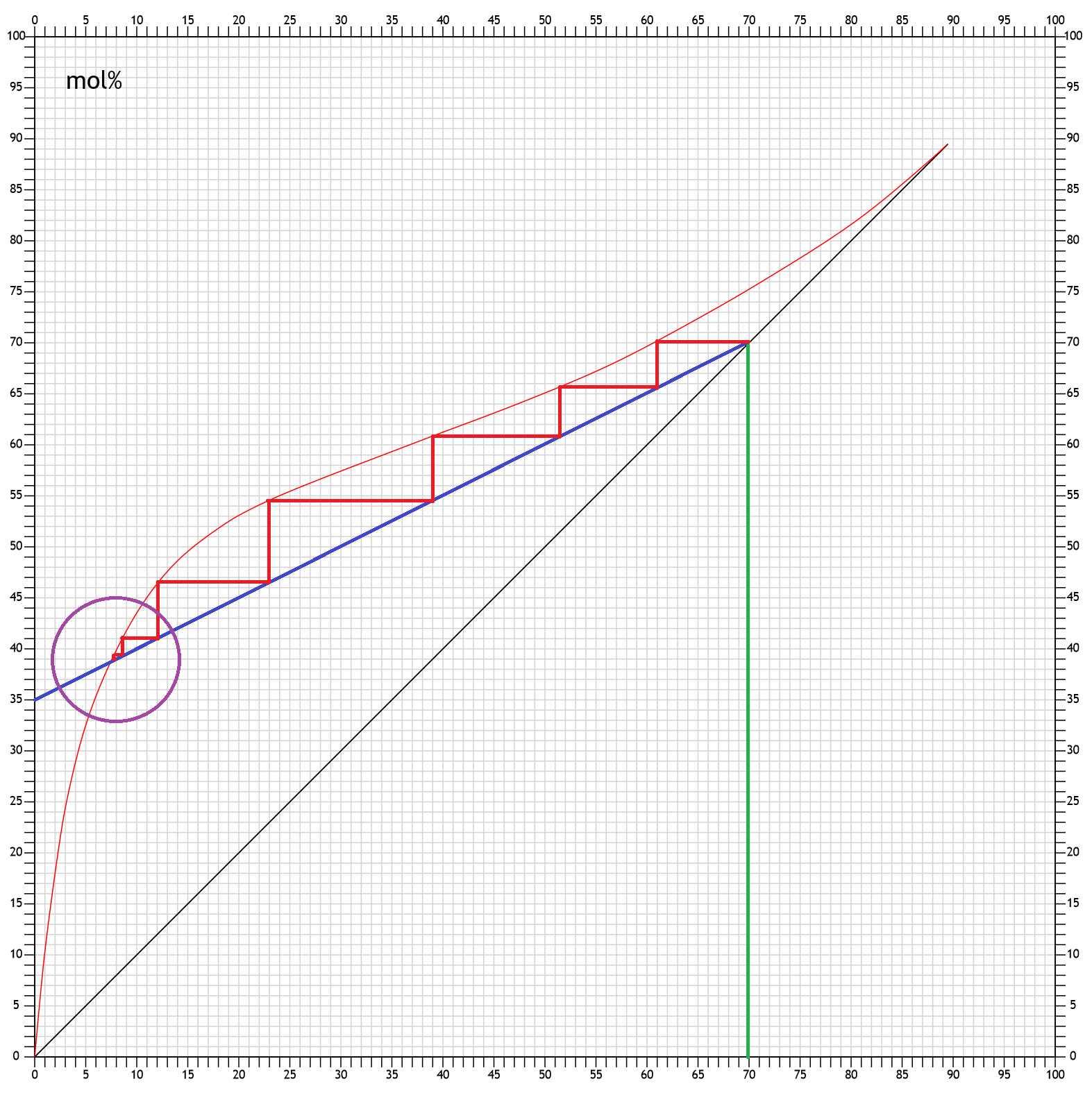
Gleichzeitig bedeutet das: Das minimale Rückflussmenge ("minimal reflux ratio"), um von 7.5mol% auf 70mol% zu kommen, ist 50% Reflux. Egal, wie viele reale Böden man hat.
So ein minimales Rückflussverhältnis lässt sich auch direkt konstruieren. Hier das minimale Rückflussverhältnis, um von 10mol% auf 75mol% zu kommen: Der Winkel der blauen Arbeitsgerade entscheidet dann über die % Reflux. In diesem Fall sind es etwa 35% Reflux.
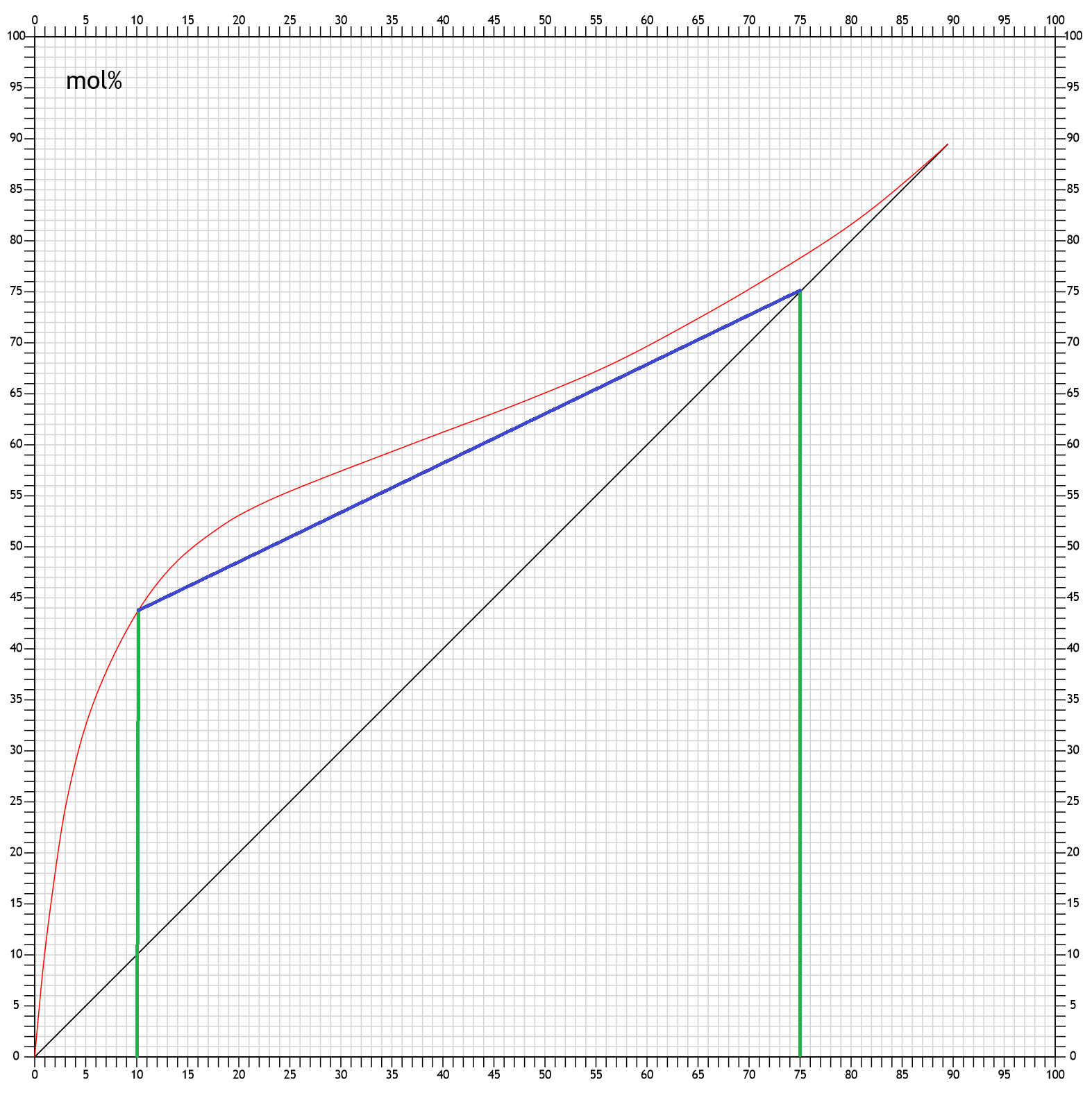
Wegen der besonderen Krümmung der Siedediagrammkurve, tritt bei noch höheren Zielalkoholstärken aber ein Problem auf: Die von 15mol% zu 80mol% gezeichnete Arbeitsgerade schneidet die Siedediagrammkurve bei etwa x = 70mol%. Das bedeutet, daß man mit dem laut Winkel der Arbeitsgeraden angegebenen Rückflussverhältnis mindestens 70mol% in der Destille benötigt, um auf 80mol% im Destillat zu kommen. Mit den geplanten 15mol% geht das nicht. Zumindest nicht mit diesem Rückflussverhältnis.
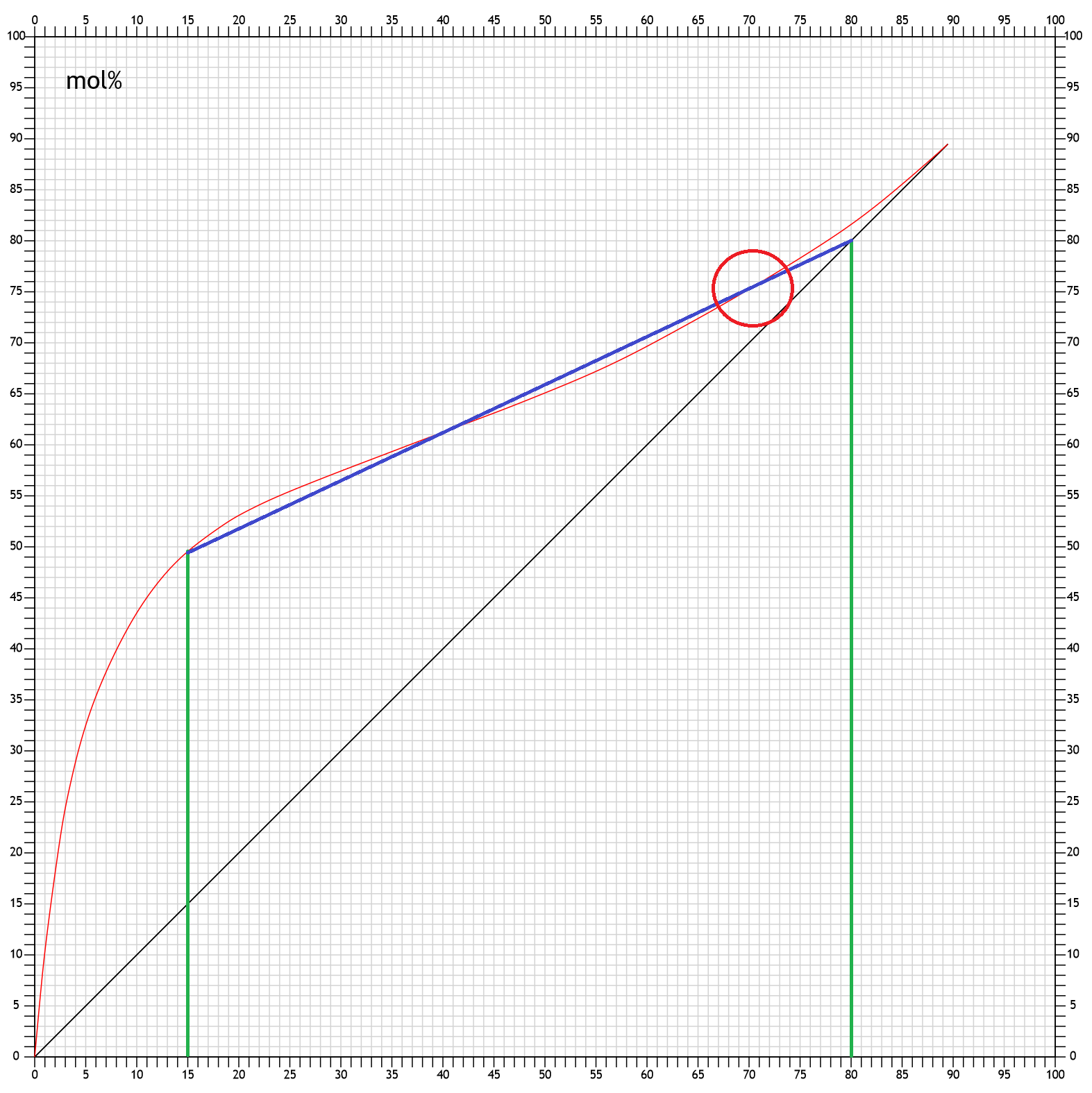
Um mit niedrigen mol% im Kessel überhaupt auf 80mol% im Destillat zu kommen, muss man also den Winkel und damit das Rückflussverhältnis ändern, bis dieser Schnittpunkt verschwindet: Hier schafft man es nun sogar mit etwa nur 9.5mol% im Kessel auf 80mol% im Destillat zu kommen. Denn die Arbeitslinie ist ganz knapp unter der Siedediagrammkurve. Dies braucht aber sehr sehr viele Böden, da dort, wo die blaue Arbeitsgerade und die Siedediagrammkurve sich sehr nahe sind, die eingezeichneten Stufen sehr klein wären und somit sehr viele Stufen Platz hätten.
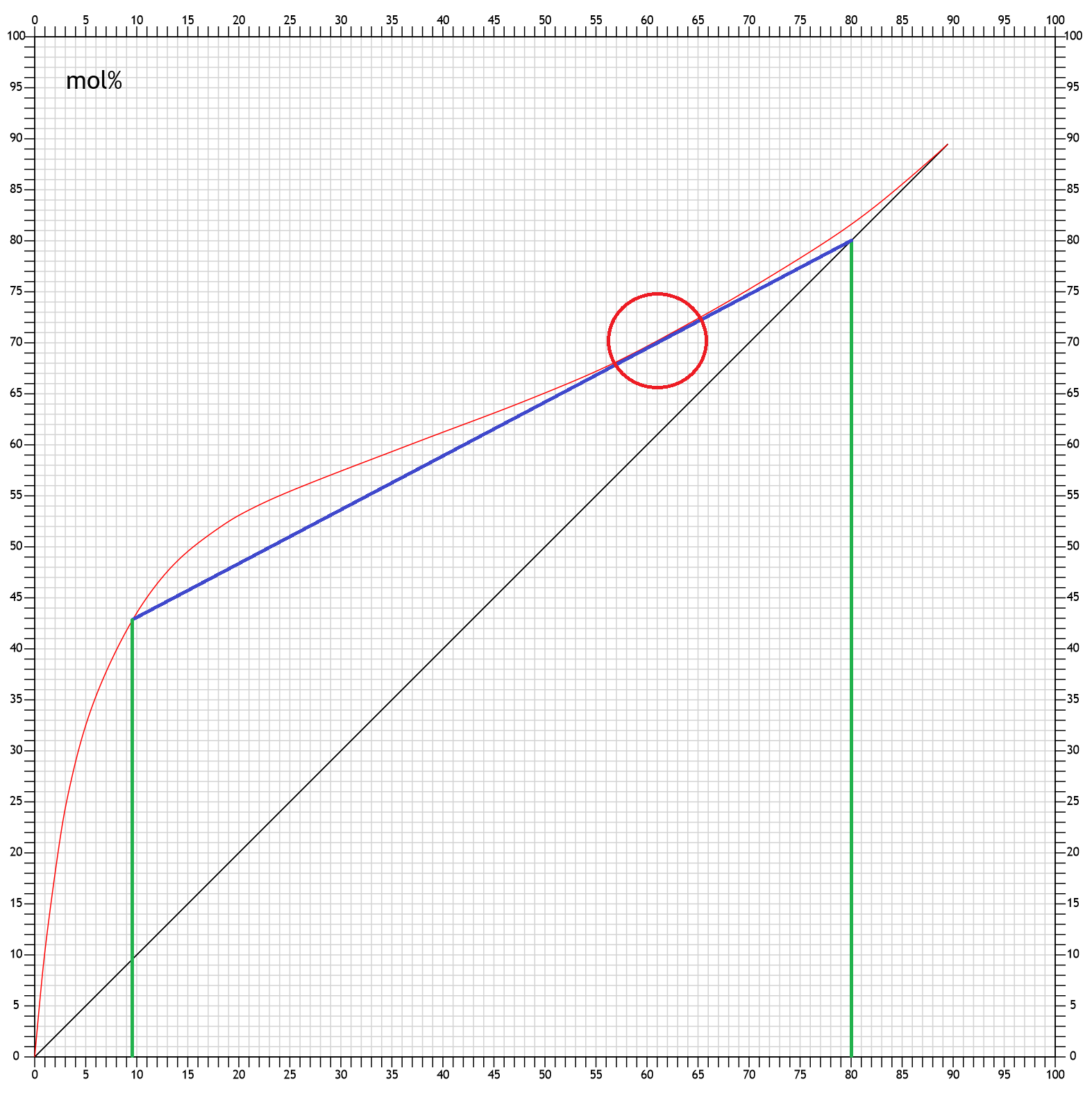
Zeichnet man die Arbeitsgerade so ein, daß sie eine Tangente zur Siedediagrammkurve bildet, nennt man den Kontaktpunkt "Pinch". Der Pinch ist in diesem Fall also etwa bei 61mol%. Das bedeutet, man braucht mindestens 61mol% im Kessel für 80mol% im Destillat bei dem Rückflussverhältnis laut dem Winkel der Arbeitsgeraden. Aber mit minimal mehr Reflux man kann mit wesentlich niedriger Alkoholstärke im Kessel die 80mol% erreichen.

Die Genauigkeit dieser Methode:
Nun stellt sich die Frage, ob so ein graphisches Verfahren wirklich die Realität abbildet. Waum sollte die Realität sich so verhalten, wie sie mit einem Diagramm und einem Lineal und Winkelmesser konstruiert werden kann? Warum nimmt man ein mol%-Siedediagramm und nicht eines basierend auf gew% oder vol%? Oder warum überhaupt ein Diagramm mit den Alkoholstärken, warum nicht mit den Siede- bzw. Dampftemperaturen? Warum besteht ein linearer Zusammenhang zwischen den Punkten 0% Reflux (Winkel der Arbeitsgerade 0°) und 100% Reflux (45°), also warum sind 22.5° dann 50% Reflux? Warum ist angesichts der nicht-linearen Siedediagrammkurve und den anderen nicht-linearen Zusammenhängen (zB. Alkoholstärke/Dampftemperatur und vol%/mol%) trotzdem alles so einfach und linear?
Die Antwort darauf: Das McCabe-Thiele-Verfahren folgt einer möglichst einfachen Logik und erreicht damit eine hohe Übereinstimmung mit der Praxis. Zumindest bei Ethanol-Wasser-Lösungen; diese Methode ist ja nicht speziell dafür gedacht. Und dies klappt ohne Computer (bei der Veröffentlichung 1925 gab es die ja auch noch nicht). Nur mit den Siedediagrammdaten, welche zumindest bei den industrierelevanten Substanzen ja schon gemessen worden waren. Es waren also keine zusätzliche Messungen nötig.
Diese Methode wird von der Industrie als Prognoseinstrument verwendet. Man berechnet, was man tun und haben muss, um möglichst ökonomisch das zu bekommen, was man möchte. Dann macht man das, und wenn das Ergebnis dann nicht ganz passt, korrigiert man nach.
Gibt es Hinweise oder Beweise, inwiefern diese Methode ungenau ist?
Die gibt es: Eine der Bedingungen, welche für ein wirklich exakt funktionierendes McCabe-Thiele-Verfahren nötig sind, ist ein sogenannter "constant molar overflow". Dieser bedeutet, pro Zeit entweicht aus jeder Platte dieselbe Stoffmenge Dampf und von jeder Platte fließt dieselbe Stoffmenge als Reflux nach unten. Stoffmenge bedeutet die Molekülanzahl, nicht das Gewicht oder Volumen. Also wenn von der ersten Platte 50 Ethanolmoleküle und 50 Wassermoleküle als Dampf nach oben gehen, gehen auch von der zweiten Platte 100 Moleküle nach oben. Mit normalerweise höherem Alkoholgehalt. Also nicht 50 Ethanol und 50 Wasser, sondern beispielsweise 65 Ethanol und 35 Wasser. Und das gleiche beim Reflux: Von jeder Platte geht dieselbe Stoffmenge nach unten. Nicht aber muss es dieselbe Stoffmenge sein, die als Dampf nach oben geht. Dieselben Stoffmengen als Dampf nach oben und als Reflux nach unten gibt es nur bei 100% Reflux. Constant molar overflow kann es aber nur geben, wenn die beteiligten Stoffe dieselbe Verdampfungsenthalpie haben. Das bedeutet bei unseren Ethanol-Wasser-Lösungen, daß es dieselbe Energie braucht, ein Ethanol- oder ein Wassermolekül zu verdampfen. Und das ist nicht ganz der Fall. Außerdem berücksichtigt McCabe-Thiele nicht die Temperaturunterschiede zwischen den aufeinandertreffenden Alkoholstärken, durch welche zusätzliche Energiebeewegungen stattfinden, welche je nachdem, wie die Temperaturkurven des Siededigramms an der konkreten Stelle ausschauen, zu zusätzlicher oder reduzierter Verdampfung führen.
Beide Punkte machen aber nicht so viel aus, daß eine Berechnung nach McCabe-Thiele bei Ethanol-Wasser-Lösungen wertlos wäre. Da wir das McCabe-Thiele-Verfahren in viele Rechner eingebaut haben, ist uns aber durchaus aufgefallen, daß die Rechnung nicht immer aufgeht. Man kann nämlich überprüfen, ob die Ergebnisse mit McCabe-Thiele mit anderen Berechnungen zusammenpassen. Dann merkt man, daß McCabe-Thiele vor allem im mittleren % Reflux-Bereich unrealistisch hohe Destillatsalkoholstärken berechnet, was in vielen Fällen sogar zur Folge hat, daß rechnerisch mehr Alkohol im Destillat landet als netto aus dem Kessel entweicht. Folgende ganz klare Regeln gelten:

1. Das, was als Dampf den Kessel verlässt, minus das, was in den Kessel zurückfließt, entspricht rechnerisch genau dem, was als Produkt abgezogen wird. Sonst würde ja etwas verschwinden oder dazukommen.
2. Wärmeverluste unberücksichtigt, liegt oben in der Kolonne dieselbe Wärmeenergie an wie im Kessel.
3. Die Dampfmenge lässt sich aus der Alkoholstärke und der zugeführten Energie sehr genau berechnen.

Und diese Rechnung passt dann nicht mehr zu den Ergebnissen mit McCabe-Thiele: Mit McCabe-Thiele berechnete Destillats-Alkoholstärken und aus dem Energieeintrag und den % Reflux dann berechnete Produktmengen, entsprechen in manchen Fällen nicht der Differenz aus dem, was den Kessel als Dampf verlässt, und dem, was in ihn als Reflux zurückfließt.
Hier ein Beispiel, teil der Forumsdiskussion Alkoholstärken, Massenströme und Temperaturen in Refluxkolonnen: Aus 9.2gew% im Kessel entstehen bei 2590 Watt 100g/min Dampf mit 50gew% (berechnet aus den Siedediagrammdaten, den 2590 Watt und den Verdampfungsenthalpien von Ethanol und Wasser). Mit fünf Böden (dem Kessel plus vier Böden) erreicht man bei 50% Reflux laut McCabe-Thiele ein Destillat mit 84.16gew%. Diese Alkoholstärke bedeutet, daß oben 145g/min Dampf ankommen (berechnet aus den 2590 Watt und den Verdampfungsenthalpien von Ethanol und Wasser). 50% davon werden als Produkt abgezogen, die anderen 50% fließen als Reflux zurück. Also wir haben 72.7g/min Destillat mit 84.16gew% und dieselbe Menge mit derselben Alkoholstärke fließt zurück in die Kolonne.
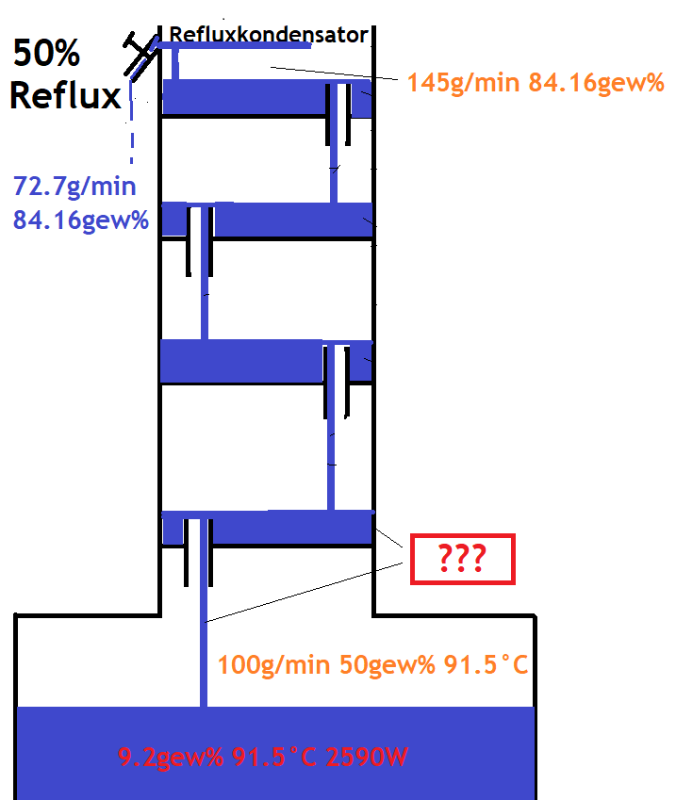
- Die Dampfentwicklung im Kessel von 100g/min mit 50gew% sind 50g/min reines Ethanol.
- Die Produktentnahme von 72.7g/min mit 84.16gew% sind 61.2g/min reines Ethanol.
Es wird also mehr Ethanol als Produkt abgezogen als unten überhaupt verdampft. Das kann natürlich nicht sein.
Dieses Problem tritt so sichtbar aber nur bei mittleren % Reflux auf. Normalerweise betreiben wir unsere Refluxdestillen aber ja mit mindestens 80% Reflux, im Schnitt vielleicht so mit 90%. Dieses Problem ist also kein Hinweis, daß das McCabe-Thiele-Verfahren in der üblichen Praxis unserer Refluxdestillationen mit Ethanol-Wasser-Lösungen stark fehlerhaft ist. Aber man sieht, daß keine mathematische Gültigkeit besteht.

Eine praktische Umsetzung des McCabe-Thiele-Verfahrens ist unser McCabe-Thiele-Kolonnensimulator. Und auch unsere anderen Rechner, bei denen die Refluxmenge eine Rolle spielt, rechnen nach diesem Verfahren.
Die Ausnahme ist unser Kolonnensimulator, welcher nicht nach McCabe-Thiele sondern mit wesentlich mehr Rechenaufwand iterativ Lösungen berechnet, welche alle uns bekannten Vorgaben einhalten, welcher also ohne die Ungenauigkeiten von McCabe-Thiele Kolonnen berechnen kann.