This method was published by Warren L. McCabe and Ernest Thiele in 1925.
It is a very easy to understand graphical method for planning distillations. It primarily deals with the continuous distillation systems that are important for the industry. However, the method can also be applied to non-continuous systems such as our reflux stills and is even easier to understand.
The valuable thing about this is that it allows the amount of reflux to be included in calculations. For example, you can calculate how the alcohol strength of the distillate decreases when more product is removed from the top of the column, thus reducing the reflux back into the column.

The construction of a McCabe-Thiele diagram for a non-continuous still:
A McCabe-Thiele diagram starts with the curve x = alcohol strength in the boiler and y = alcohol strength in the distillate, i.e. a boiling diagram curve, and an diagonal line at x = y: Then the target alcohol strength in the distillate is entered as a vertical line from the bottom up to the diagonal straight line. In the next picture at x = 70%abm (alcohol by mol concentration). And then, starting from the reached point to the left, a so-called "operating line" is drawn in. Its angle indicates the reflux amount. If it goes horizontally to the left, this means 0% reflux, i.e. a potstill or a reflux still with the reflux switched off. If it goes 45° down to the left, i.e., if it lies on the black diagonal straight line, this means 100% reflux. Angles outside this range are not possible. Exactly in the middle between horizontal and 45°, i.e. at 22.5°, means 50% reflux. This is also how it is drawn here: And now the real trays are drawn in as steps and a line is drawn all the way down at the end. Assuming the still has 5 real plates or the equivalent in pack height, this is what it looks like: The left green line is at about x = 12%abm.
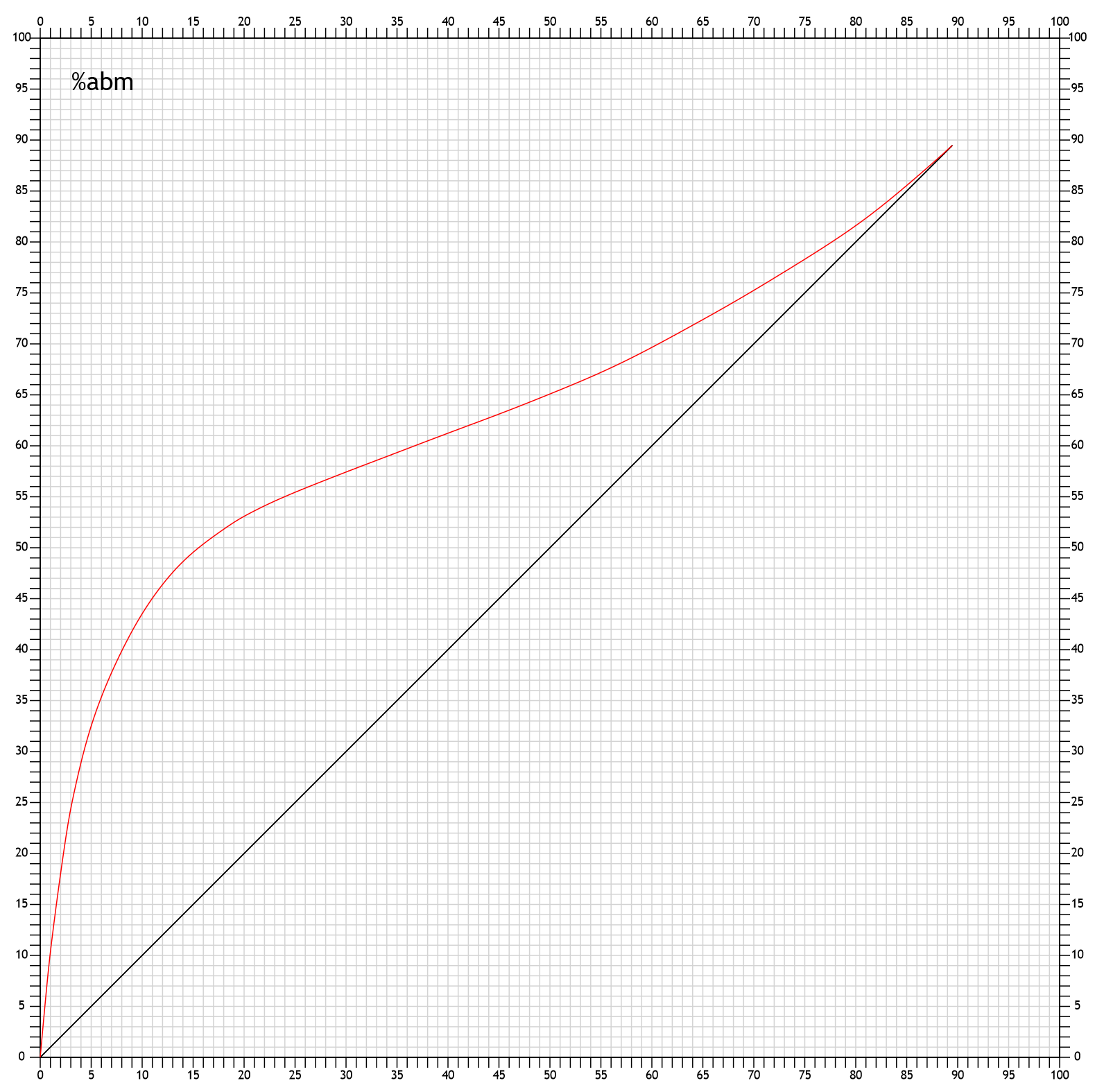
So the result is:
To get to 70%abm with 50% reflux (i.e., a reflux ratio of 1) with 5 plates, you need 12%abm in the still.
Or:
If you have 12abm% in a still with 5 trays, then with 50% reflux you get a distillate with 70%abm. But you can't construct the diagram this way. You always have to construct it starting from a distillate alcohol strength. To calculate the distillate alcohol strength from a boiler alcohol strength, you have to iterate. So you have to estimate the result, then calculate the steps down from the distillate alcohol strength as given, use the result to correct the initial estimate, check down again, and so on. The same applies if you want to calculate the required % reflux from the two alcohol strengths and the real plates, or the required real plates from the two alcohol strengths and the % reflux.

The minimal reflux ratio:
An interesting point in the diagram is where the blue operating line intersects the boiling diagram curve. In our diagram, this is at about 7.5%abm in the boiler. The stages cannot go beyond this point. So even infinite steps would not go lower than x = 7.5%abm: This means: No matter how many plates you have, you need at least 7.5mol% in the kettle to get 70%abm in the distillate with 50% reflux. Or: To get 70%abm in the distillate with lower alcohol strength in the boiler, it is mandatory to increase the reflux.
At the same time this means: The minimum reflux amount to get from 7.5%abm to 70%abm is 50% reflux. No matter how many real plates you have.
Such a minimal reflux ratio can also be constructed directly. Here is the minimum reflux ratio to get from 10%abm to 75%abm: The angle of the blue operating line then determines the % reflux. In this case, it is about 35% reflux.
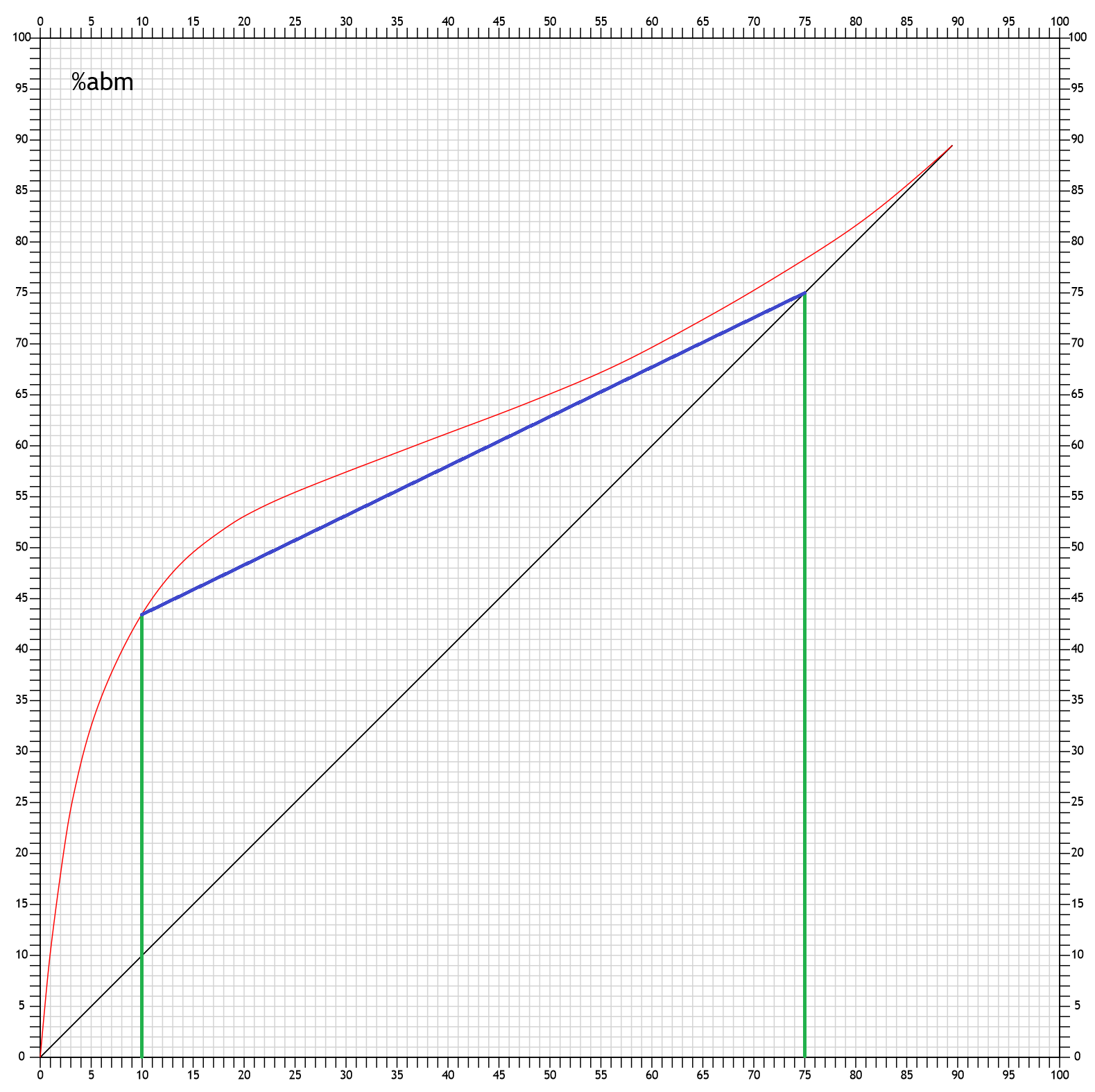
Because of the special curvature of the boiling diagram curve, however, a problem occurs at even higher target alcohol strengths: The operating line drawn from 15mol% to 80mol% intersects the boiling diagram curve at about x = 70%abm. This means that with the reflux ratio given according to the angle of the working line, you need at least 70%abm in the boiler to get to 80%abm in the distillate. With the planned 15%abm this is not possible. At least not with this reflux ratio.
So to get to 80%abm in the distillate at all with low %abm in the boiler, you have to change the angle, and thus the reflux ratio, until this intersection disappears: Here, even with only 9.5%abm in the boiler, it is possible to reach 80%abm in the distillate. This is because the operating line is very just below the boiling diagram curve. But this needs a lot of plates, because where the blue operating line and the boiling diagram curve are very close to each other, the steps drawn in would be very small and thus there would be room for a lot of steps.
If the operating line is drawn in such a way that it forms a tangent to the boiling diagram curve, the contact point is called a "pinch". In this case, the pinch is at about 61%abm. That means you need at least 61%abm in the kettle for 80%abm in the distillate at the reflux ratio according to the angle of the operating line. But with minimal more reflux one can reach the 80%abm with much lower alcohol strength in the boiler.

The accuracy of this method:
Now the question arises whether such a graphical method really represents reality. Why should reality behave as it can be constructed with a diagram and a ruler and protractor? Why take a %abm boiling diagram and not one based on weight percent or volume percent? Or why use a diagram with the alcohol strengths at all, why not with the boiling or vapor temperatures? Why is there a linear relationship between the points 0% reflux (angle of the working line 0°) and 100% reflux (45°), so why is 22.5° then 50% reflux? Given the non-linear boiling diagram curve and the other non-linear relationships (e.g. alcohol strength/steam temperature and %abv/%abm), why is everything so simple and linear anyway?
The answer: The McCabe-Thiele method follows the simplest possible logic and thus achieves a high degree of agreement with practice. At least with ethanol-water solutions; this method is not specifically designed for this purpose. And this works without the necessity of computers (at the time of publication in 1925 they did not exist yet). Only with the boiling diagram data, which had already been measured at least for the industrially relevant substances. So no additional measurements were necessary.
This method is used by the industry as a prognosis tool. You calculate what you have to do and have to have in order to get what you want as economically as possible. Then you do that, and if the result doesn't quite fit, you make corrections.
Is there any evidence or proof that this method is inaccurate?
There is: One of the conditions required for a truly accurate McCabe-Thiele method is a so-called "constant molar overflow". This means that the same amount of substance evaporates from each plate per time and the same amount of substance flows down from each plate as reflux. Amount of substance means the number of molecules, not the weight or volume. So if 50 ethanol molecules and 50 water molecules evaporate from the first plate, 100 molecules also evaporate from the second plate. Normally with a higher alcohol content. So not 50 ethanol and 50 water, but 65 ethanol and 35 water, for example. And the same with reflux: The same amount of substance flows downwards from each plate. However, it does not have to be the same amount of substance that evaporates. The same amount of substance evaporating and flowing down as reflux happens only at 100% reflux. However, constant molar overflow can only occur if the substances involved have the same enthalpy of vaporization. In the case of our ethanol-water solutions, this means that it takes the same energy to vaporize an ethanol or a water molecule. And this is not quite the case. Furthermore, McCabe-Thiele does not take into account the temperature differences between the interacting alcohol strengths, through which additional energy movements take place, which lead to additional or reduced evaporation depending on how the temperature curves of the boiling digram look at the specific point.
However, both points do not make so much difference that a calculation according to McCabe-Thiele would be worthless for ethanol-water solutions. But since we have built the McCabe-Thiele method into many computers, we have noticed that the calculation does not always work. Namely you can verify whether the results with McCabe-Thiele fit together with other calculations. Then you realize that McCabe-Thiele calculates unrealistically high distillate alcohol strengths, especially in the middle % reflux range, resulting in many cases in more alcohol ending up in the distillate than the net amount leaving the boiler. The following very clear rules apply:

1. What leaves the boiler as vapor minus what flows back into the boiler corresponds exactly to what is pulled off as product. Otherwise, something would disappear or be added.
2. If heat losses are not taken into account, the same heat energy is present at the top of the column as in the boiler.
3. The amount of vapor can be calculated very accurately from the alcohol strength and the supplied energy.

And this calculation then no longer fits the results with McCabe-Thiele: Distillate alcohol strengths calculated with McCabe-Thiele and product quantities then calculated from the energy input and the % reflux do not correspond in some cases to the difference between what leaves the boiler as vapor and what flows back into it as reflux.
Here is an example, part of the German language forum discussion Alkoholstärken, Massenströme und Temperaturen in Refluxkolonnen: From 9.2%abw in the boiler, 100g/min vapor with 50%abw is produced at 2590 watts (calculated from the boiling diagram data, the 2590 watts and the specific enthalpies of evaporation of ethanol and water). With five plates (the boiler plus four plates), a distillate of 84.16%abw is obtained at 50% reflux according to McCabe-Thiele. This alcohol strength means that 145g/min of vapor arrive at the top (calculated from the 2590 watts and the specific enthalpies of evaporation of ethanol and water). 50% of this is taken off as product, the other 50% flows back as reflux. So 72.7g/min with 84.16%abw flow back.
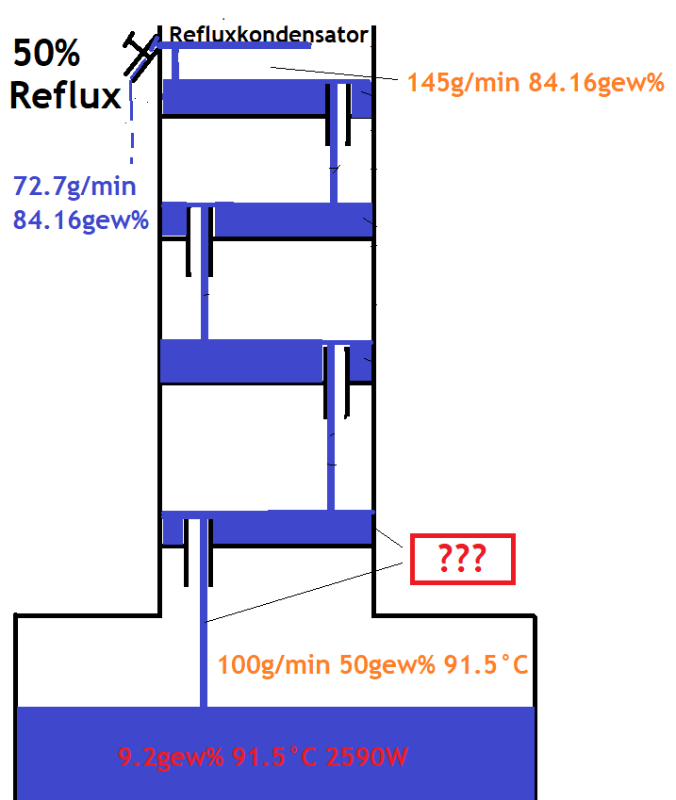
- Boiler vapor production of 100g/min at 50%abw is 50g/min of pure ethanol.
- The product take off of 72.7g/min with 84.16%abw is 61.2g/min pure ethanol.
Thus, more ethanol is drawn off as product than evaporates at all at the bottom. This cannot be the case, of course.
However, this problem only occurs so visibly with medium % reflux. Normally, we operate our reflux stills with at least 80% reflux, on average perhaps with 90%. So this problem is not an indication that the McCabe-Thiele method is flawed in the usual practice of our reflux distillations with ethanol-water solutions. But one can see that there is no mathematical validity.

A practical implementation of the McCabe-Thiele method is our McCabe-Thiele Column Simulator. And our other calculators, in which the reflux rate is a factor, also use this method.
The exception is our Column Simulator, which does not use McCabe-Thiele but calculates solutions iteratively with considerably more calculation effort, which comply with all of our known guidelines, i.e. which can calculate columns without the inaccuracies of McCabe-Thiele.